Market Crashes and Log Periodic Power Law Behavior
I read the book "Why Stock Markets Crash" by Didier Sornette and found much food for thought. Didier brought his understanding of complex systems with internal feedback mechanisms to the understanding of why markets become unstable and seem to periodically crash. Examples of crashes are 1987, 1929, 2000, May 2010, 2008 and many others. Warning: for the mathematically challenged this is a challenging book to read. Perhaps the gist can be obtained however.
Most of the time the market players go about their business in an uncoordinated fashion. The small players act as noise trades giving the market the appearance of background noise. Then every once in a while our herding mentality takes over and we begin marching in the same direction. At these times the market begins to go up super exponentially obeying a power law increase. The herding of individual investors provides the feedback mechanism leading to instability. This happens until we approach a critical instability and some piece of news provides the excuse for the market to crash. Didier found that as in nature (large earthquakes for example) there is a signature accompanying the months and years leading up to the crash that obeys the power law increase as mentioned but super imposed with a log periodic oscillation where the frequency of oscillation increases as the critical moment is approached. This can be seen in the charts and indeed the time of collapse can be estimated long before the arrival of the moment. Below is an equation showing a power law term with an "m" exponent and a superimposed oscillatory term with a cosine. t is current time and tc is the estimated time of an approaching singularity (crash.)
LPPL(t) = A+B(t-tc)^m * [1+C cos(ω ln(t-tc)/T) ]
Using excel I manually fit this equation to the timeframe approaching the October 1987 S&P500 crash. The chart ends just as the crash was starting. It is notoriously difficult to fit multiple variable equations to a set of noisy data but the fit isn't bad here. Based on the fit, the crash date estimate is 1987.761 in decimal year format (10/6/1987). In the book Didier had a better fit with a crash prediction a little later closer to the actual date. He is a more mathematically adept than I. I wanted to see if a novice however could find the periodic log power law structures and determine that a crash was being set up and make predictions. As t approaches tc the frequency of oscillations approach infinity and finally a singularity at tc. It is normal to see the LPPL function go vertical as the market begins to crash. Didier included many-many examples of market crashes from multiple countries and indexes as well as some individual stocks. The log-periodic structure continues on the other side of the crash if you replace (t-tc) by (tc-t) and the bottom and bounce times can be estimated with amazing accuracy.
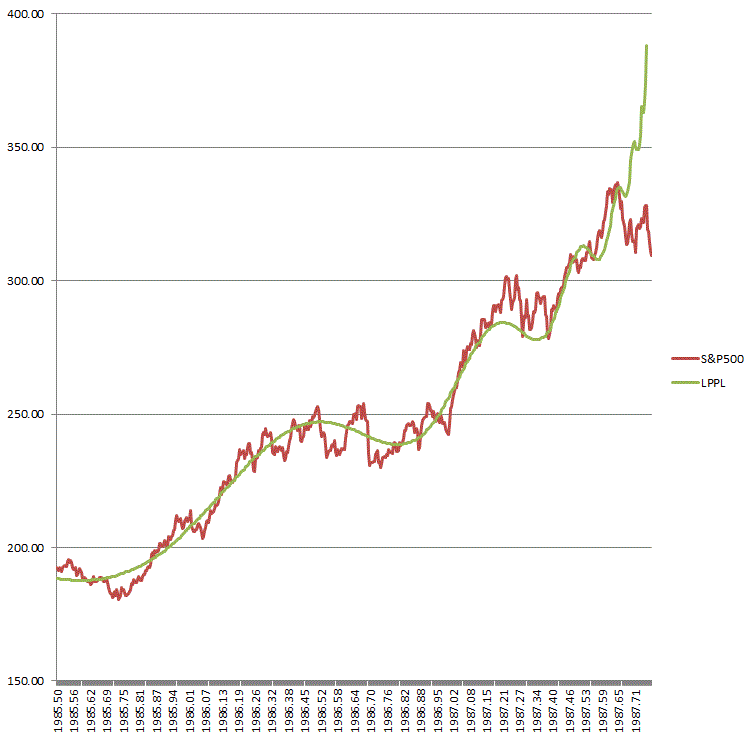
The fitting procedure is a follows:
1. Fit the daily price data to a power law function y(t) = A + B(t)^m and to an exponential law function y'(t) = A + By'(t-1). If the data fits the power law better than exponential law by variance comparison then you are in a power law market regime and you can go to step 2.
2. Fit the price data to the log periodic power law equation above. Once a best fit has been achieved all variables are determined and the approximate time of crash is known. Using this approach it should have been possible to make these determinations five months in advance of the event with ever increasing precision as more data confirms. My own method of fitting is manual observing the chart and fit with guidance of a variance computation.
Mike Scott
Cloverdale, CA



 Reply With Quote
Reply With Quote
